:::: MENU ::::
Aug 10, 2017    |       2 comments

Wybór odpowiedniego kodu odpowiedzi HTTP – przestań utrudniać sobie życie!

Poniższy tekst jest mniej lub bardziej udanym tłumaczeniem artykułu Choosing an HTTP Status Code — Stop Making It Hard :).

Nie ma rzeczy prostszej niż zwrócenie kodu odpowiedzi HTTP. Strona się wyświetliła? Świetnie, zwróćmy kod 200. Strona nie istnieje? To kod 404. Przekierowujemy użytkownika na inną stronę? No to 302 albo 301.

Życie jest piękne dopóki ktoś powie Ci, że nie używasz REST-a. Nie możesz w nocy spać, bo zastanawiasz się, czy Twoja aplikacja zwraca zgodny z REST-em i zatwierdzony przez Roya Fieldinga kod odpowiedzi. Czy wystarczy 200? Czy powinien to być raczej 204 No Content? Nie, na pewno to powinien być 202 Accepted… a może jednak 201 Created?

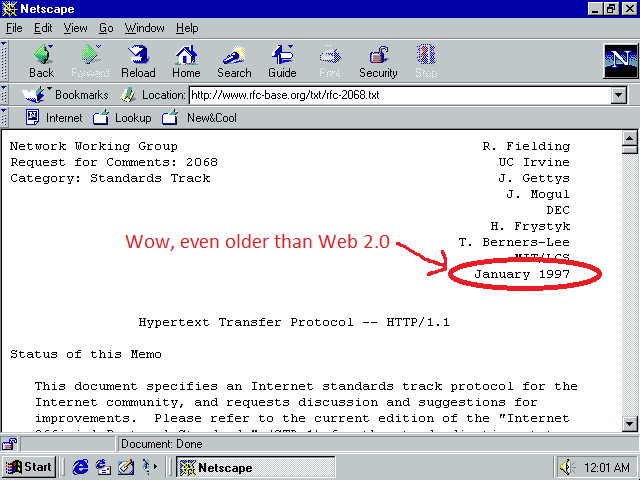
To co komplikuje nam sytuację, to oficjalny standard HTTP/1.1, RFC, które pierwotnie powstało w 1997 roku (nie zawracaj sobie głowy RFC 2616, ani tym bardziej RFC 2068, zobacz RFC 7231). 1997 to rok, kiedy zacząłem przeglądać internet na Netscape Navigator i swoim modemie 33,6 kbps. To trochę jak używać Sztuki wojennej Sun Zi do współczesne strategii biznesowej. Nieśmiertelne rady, ale nie wyobrażam sobie jak wykorzystać pięć sposobów walki ogniem do testowania rynku.

Gdyby tylko istniał jakiś wizualny sposób na wybranie tylko tych istotnych kodów?

Proszę bardzo, internecie. Ten dzień nadszedł!

Continue Reading

Mar 4, 2017    |      0 comments

RegExp likwidujący zawieszki

This one is not in english since related to polish texts only 🙂

Zawieszki to pojedyncze znaki zostawione na końcu linijki – takie jak i, z, w, itd. Ze względu na Polską Normę składania tekstu, zostawianie takich znaków na końcu wiersza jest błędem.

Chodzi o to, żeby mieć jednego regexpa, który usuwa zawieszki w zwykłym tekście, ale i w htmlu, w taki sposób, żeby nie patrzył w tagi.

(?(?=.*[<>].*)\s+([ziowauZIOWAU])\s+(?=[^>]*<)|\s+([ziowauZIOWAU])\s+)

Tutaj ciekawym trikiem jest wykorzystanie ifa i sprawdzenie czy tekst przypomina HTML czy nie.

Co więcej założeniem tego regexpa jest to, żeby przypadkiem nie mieszał w tagach html, tylko w samym tekście. Na przykład, żeby nie zamienił <span class=”elem i elem2″> na <span class=”elem i&nbsp;elem2″>

Można się tym rozwiązaniem pobawić tutaj.

Feb 9, 2017    |      0 comments

Repetitive rsync

Some time ago I’ve been moving from one hosting provider to another. I had to transfer the files from A to B and used rsync for that. But unfortunately rsync command was crashing due to some timeouts. So I’ve found really nice script for auto restore.

rsync-auto.sh

#!/bin/bash

while [ 1 ]
do
    /usr/bin/rsync -avz --progress $1 $2
    if [ "$?" = "0" ] ; then
        echo "rsync completed normally"
        exit
    else
        echo "Rsync failure. Backing off and retrying..."
        sleep 10
    fi
done

Execute

rsync-auto.sh SOURCE DESTINATION

source: stackoverflow.com

Jun 16, 2016    |      0 comments

Generating lottery codes – how many combinations will I have?

Here is a task. You have to prepare the schema for lottery codes. You have to generate lets say 1 000 000 codes that are 6 characters long. Client’s question is ‘Is that safe?’. This is a good question and you have to do some basic math to be sure that the combination of the code length and alphabet size give you enough combinations so users can’t guess other codes.

Simple example

Alphabet: A, B
Code length: 3 characters

So we have possible combinations:

AAA
AAB
ABA
ABB
BBB
BBA
BAA
BAB

So we have 8 possible combination for 3 characters code with 2 characters alphabet.

23 = 8

Later on, if we have 11 characters in our alphabet and 9 character code we will have

119 = 2 357 947 691

so if client wants 1 000 000 of codes, this scheme seems to be quite secure since is like 0,0424% of all possible combinations.

Pages:‹123456›